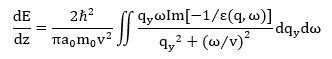Fast electrons from the incident electron beam are inelastically scattered by atomic electrons, collective oscillations of free electrons and vibrational excitation modes between atomic groups. Classical dielectric theory accurately predicts the total inelastic scattering probability i.e. the ratio of the number of electrons that scatter inelastically to the total number of electrons in the beam, by these mechanisms. Therefore, it helps predict the EELS spectrum when an electron transmits through the bulk or aloofly passes through vacuum near a surface of the material of interest.
In this theory, the interaction of a transmitted electron with the entire solid is described in terms of a dielectric response function ε (q, ω). In 1957, Ritchie derived an expression for the electron scattering power of an infinite medium. The stopping power (dE/dz) is equal to the backward force on the transmitted electron in the direction of motion and is also the electronic charge multiplied by the potential gradient in the z-direction. Using Fourier transforms, Ritchie showed that
where the angular frequency ω is equivalent to E/ℏ, a0 is the first Bohr radius, m0 is the mass of the electron and qy is the component of the scattering vector in a direction perpendicular to velocity v. The imaginary part of [−1/ε (q, ω)] is known as the energy-loss function and provides a complete description of the response of the medium through which the fast electron is traveling. The stopping power can be related to the double-differential cross section (per atom) for inelastic scattering by
where na represents the number of atoms per unit volume of the medium. For small scattering angles, dqy ≈ k0θ and dΩ ≈ 2πθdθ, so,
where θE = E/(γm0v2), γ = √(1-v2/c2), is the characteristic angle for a particular energy loss E. In the small-angle dipole region, ε (q, E) varies little with q and can be replaced by the optical value ε (0, E), which is the relative permittivity of the specimen at an angular frequency ω = E/ℏ. An energy-loss spectrum that has been recorded using a reasonably small collection angle can, therefore, be compared directly with optical data. Such a comparison involves a Kramers–Kronig transformation to obtain Re [1/ε (0, E)], leading to the energy dependence of the real and imaginary parts (ε1 and ε2) of ε (0, E). At large energy loss, ε2 is small and ε1 close to 1, so that Im(−1/ε) = ε2/(ε12 + ε22) becomes proportional to ε2 and (apart from a factor of E−3) the energy-loss spectrum is proportional to the x-ray absorption spectrum.
The optical permittivity is a transverse property of the medium, in the sense that the electric field of an electromagnetic wave displaces electrons in a direction perpendicular to the direction of propagation, the electron density remaining unchanged. On the other hand, an incident electron produces a longitudinal displacement and a local variation of electron density. The transverse and longitudinal dielectric functions are precisely equal only in the random-phase approximation at sufficiently small q (Nozieres and Pines, 1959); nevertheless, there is no evidence for a significant difference between them, as indicated by the close similarity of Im(−1/ε) obtained from both optical and energy-loss measurements on a variety of materials (Daniels et al., 1970).
– R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, 2nd ed. (New York: Plenum/Springer, 1996).